🚀 Intro
Imagine having lovable animals serve as a major and viable method of transportation.
If you did not already know, Pokémon is one of the, if not the, highest-grossing media franchises. In this fictional universe, humans coexist with living creatures known as Pokémon. Across various animated series, movies and video games, humans may use the elemental powers of Pokémon to fly between cities and towns, and travel across bodies of water.
While a general audience of any media adopts a certain level of suspension of disbelief, I find it fun to closely examine how realistic or unrealistic the world-building is. In this project, I analyzed over 1000 Pokémon to determine whether they could reasonably serve as our personal aircraft or surfboat.
Fastforwarding ahead, check out my Bulbapedia Web Scraper repository on Github!
Credits to the YouTube channel adef because he made two videos discussing this very topic:
- Mathematically Proving which Pokémon Should Learn Fly
- Mathematically Proving which Pokémon Should Learn Surf
In each video, adef explained the physics concepts involved and how he went about conducting his research, which I will try my best to explain in my own words. Throughout your reading journey, I will also include buttons to reveal some supplementary information. These only provide additional information and are not mandatory - but I highly recommend reading them!
For transparency, adef mentioned he has a Master's degree in physics (!!!), and the last physics course I took was an introductory physics course in university. So, at most, I have high-school/first-year physics knowledge...
This is to say that I'm not an expert!
This project will roughly cover forces, buoyancy, density, birds, flight, and bird flight. And I aimed to try to have some fun when discussing them.
I do not own any aspect of Pokémon, and no copyright or trademark infringement is intended. All rights go to the Pokémon Company, GAME FREAK, Creatures Inc., and Nintendo.
I also do not own Bulbapedia. Please see Bulbapedia's:
🏆 Goals
Science and Pokémon is a niche combination that is right up my alley! As aforementioned, I thought it would be fun to apply real-world physics into the Pokémon universe.
As well, this served as another opportunity to practice the python language and data-scrapping methods.
⏳ Development
Like adef's videos, I targetted Fly and Surf. These are two elemental moves that only a portion of Pokémon can learn and perform. They are primarily attacks that deal damage but in addition, Fly acts like air travel, and Surf acts like water transportation. Specifically in the video games, we use Fly to fast travel and Surf to cross bodies of water. Notably, the playable character does not have access to a personal plane/balloon/aircraft or boat/swim equipment.
Alright, it's science time! Let's start with some of the physics for Fly.
In short, a force is an external influence acting on an object, such as frictional force, pushing a shopping cart, or the force due to gravity. Forces can be easily visualized using a free-body diagram:
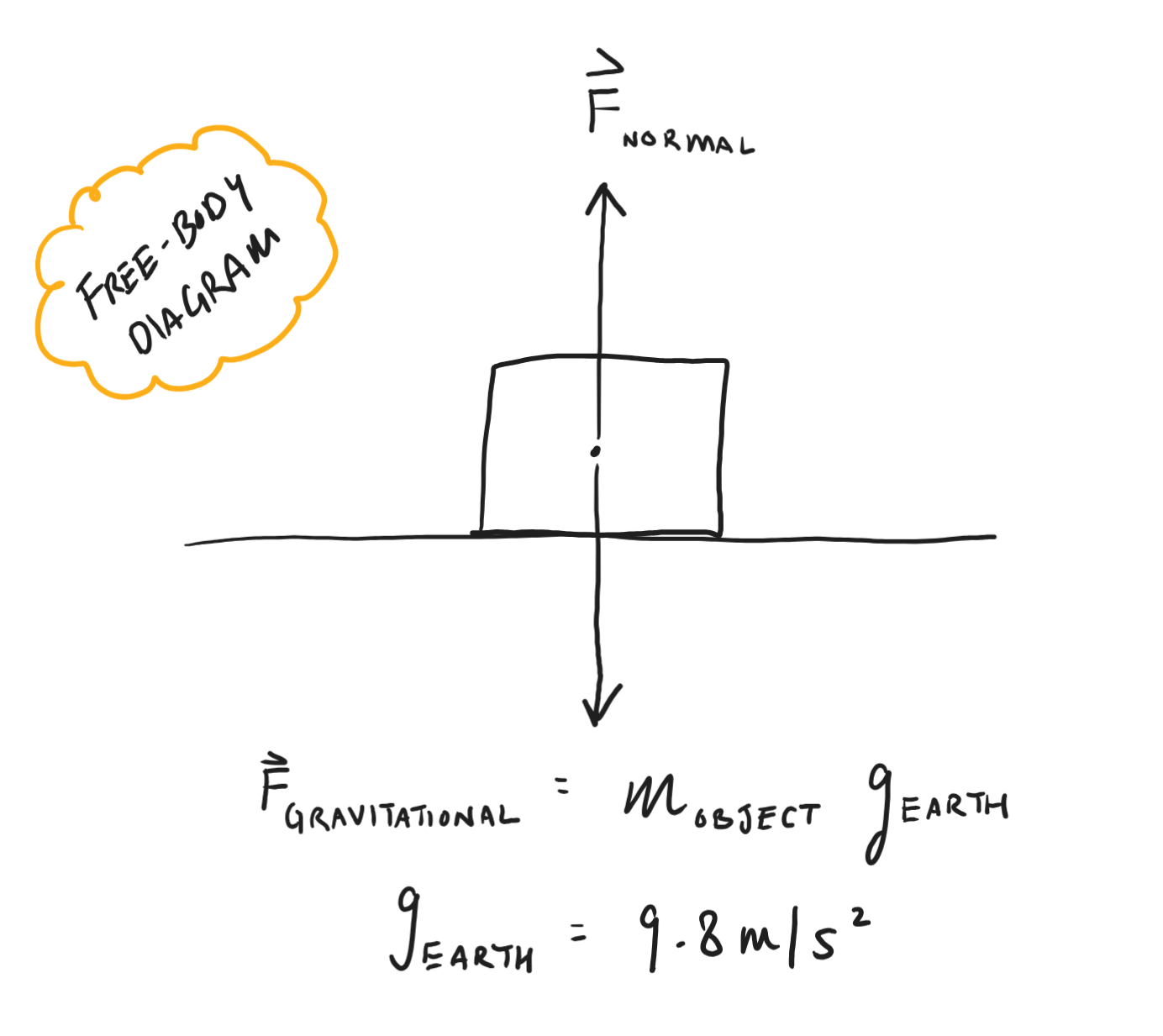
Forces acting on an object on a surface:
- \( \text F_\text{Normal} =\) force acting on an object that is perpendicular to the surface that the object contacts
-
\( \text F_\text{Gravitational} =\) weight force \(=\) force acting on object by the planet's gravity
- \( \text F_\text G =\) object mass \(\times g\)
- \(\ g =\) acceleration due to gravity
- \(g_\text{Earth} = 9.8\ m/s^2 \)
For something to float or fly, it must overcome its weight force. In flight, there are four primary forces at play:
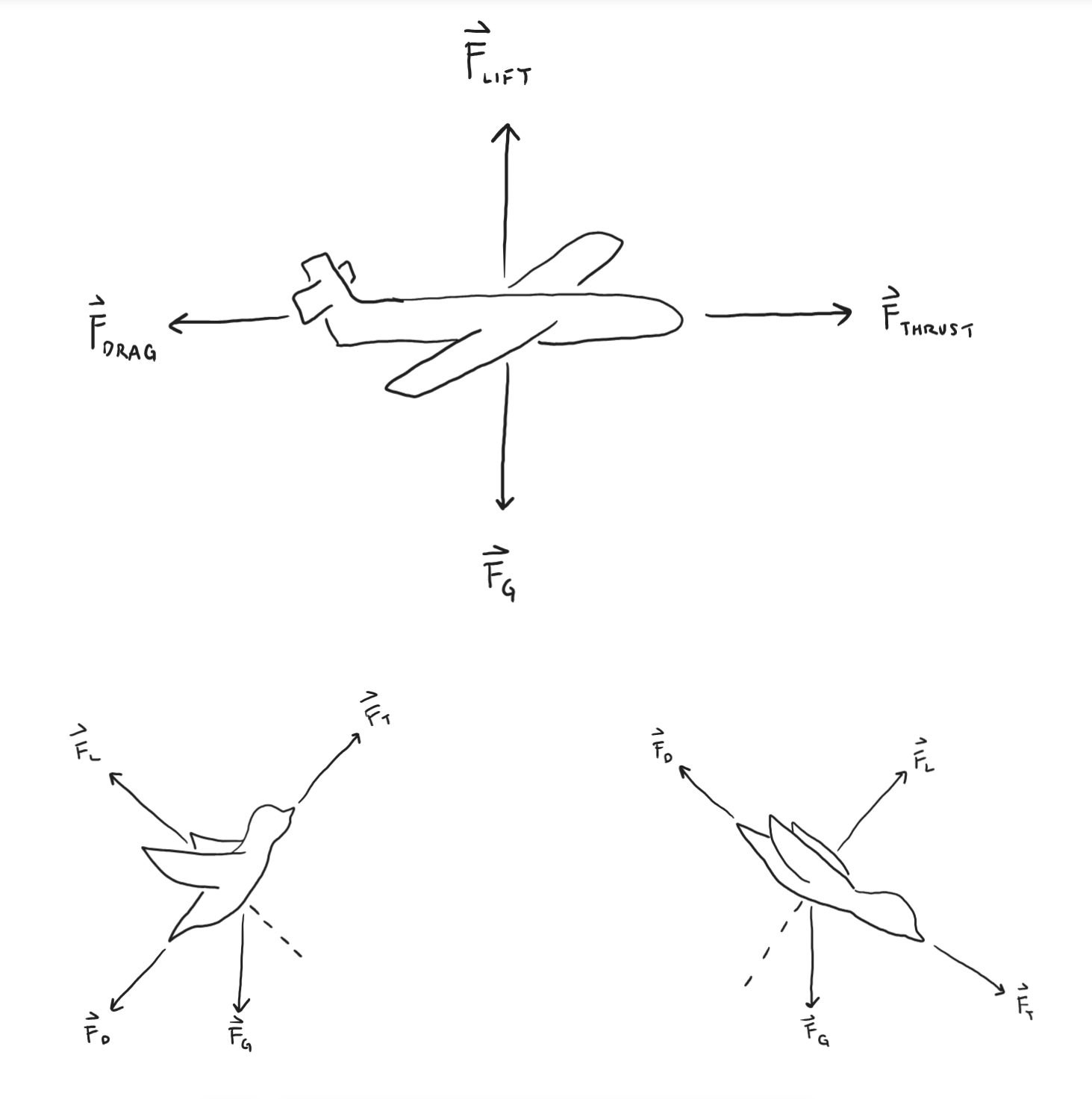
- \( \text F_\text{Lift}\)
- \( \text F_\text{Thrust}\)
- \( \text F_\text{Gravitational}\)
- \( \text F_\text{Drag}\)
Fluid dynamics is also involved in flight. In physics, a fluid can be a liquid or gas.
- \(P =\) pressure
- \(\rho =\) density
- \(v =\) velocity
- \(g =\) acceleration due to gravity
- \(h =\) height
Bernoulli's princple, derived from the Conservation of Energy, explains how airplanes achieve lift. The equation relates a fluid's speed, height and pressure.
- Faster fluid = lower pressure
- Slower fluid = higher pressure
- \(P =\) pressure
- \(F =\) force
- \(A =\) area
Pressure is the amount of force exerted on the surface of an object. By rearranging the equation, we can also say that the force on an object is equal to the pressure over the area.
Fluids naturally seek equilibrium in pressure if there exist pressure differences in a system. As a result, fluids in the area with high pressure will move along the path of least resistance towards the area with low pressure.
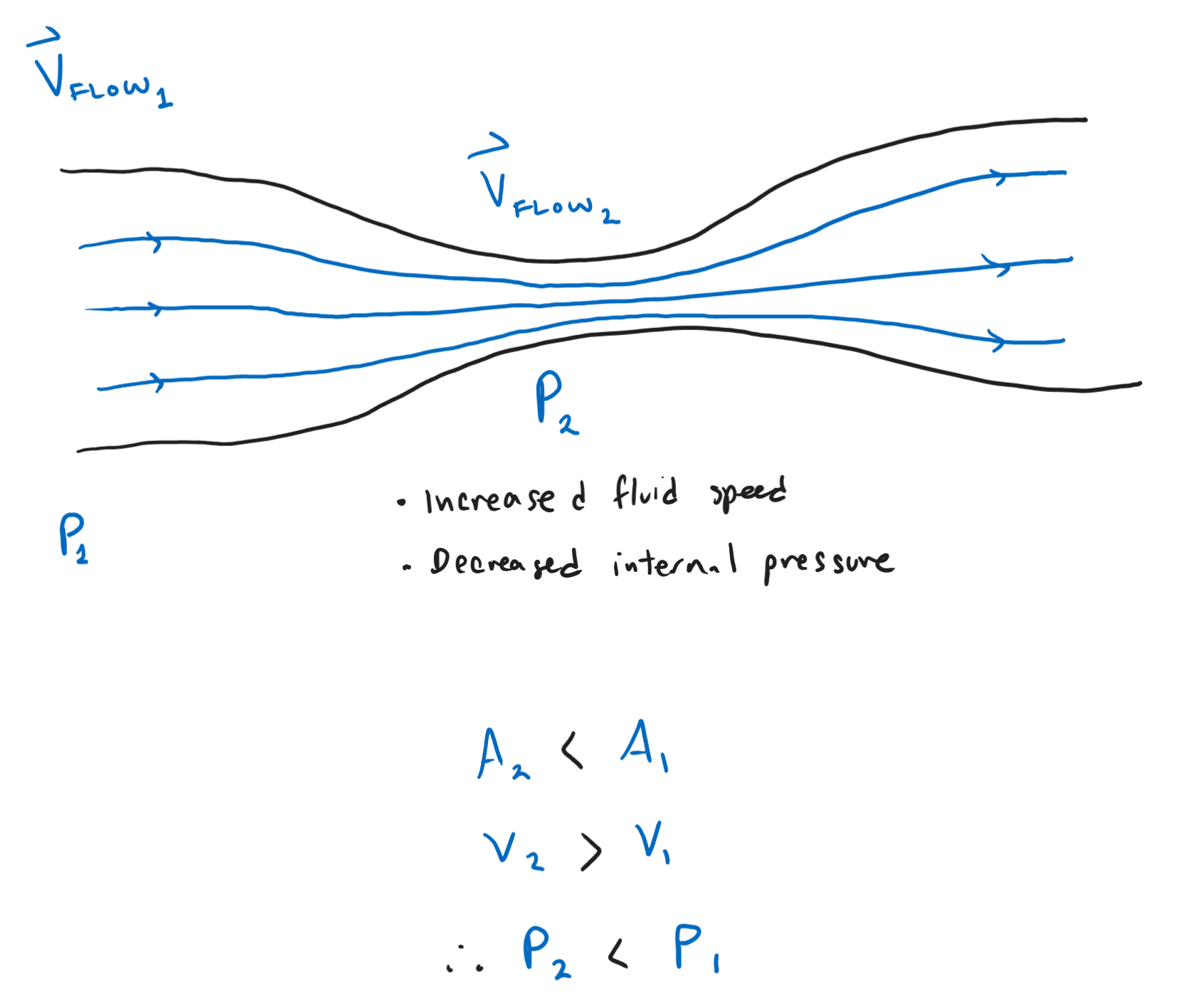
As an airplane speeds up via thrust, the material and the shape of the wings will cause a different flow of air above and below. And this causes a pressure difference!
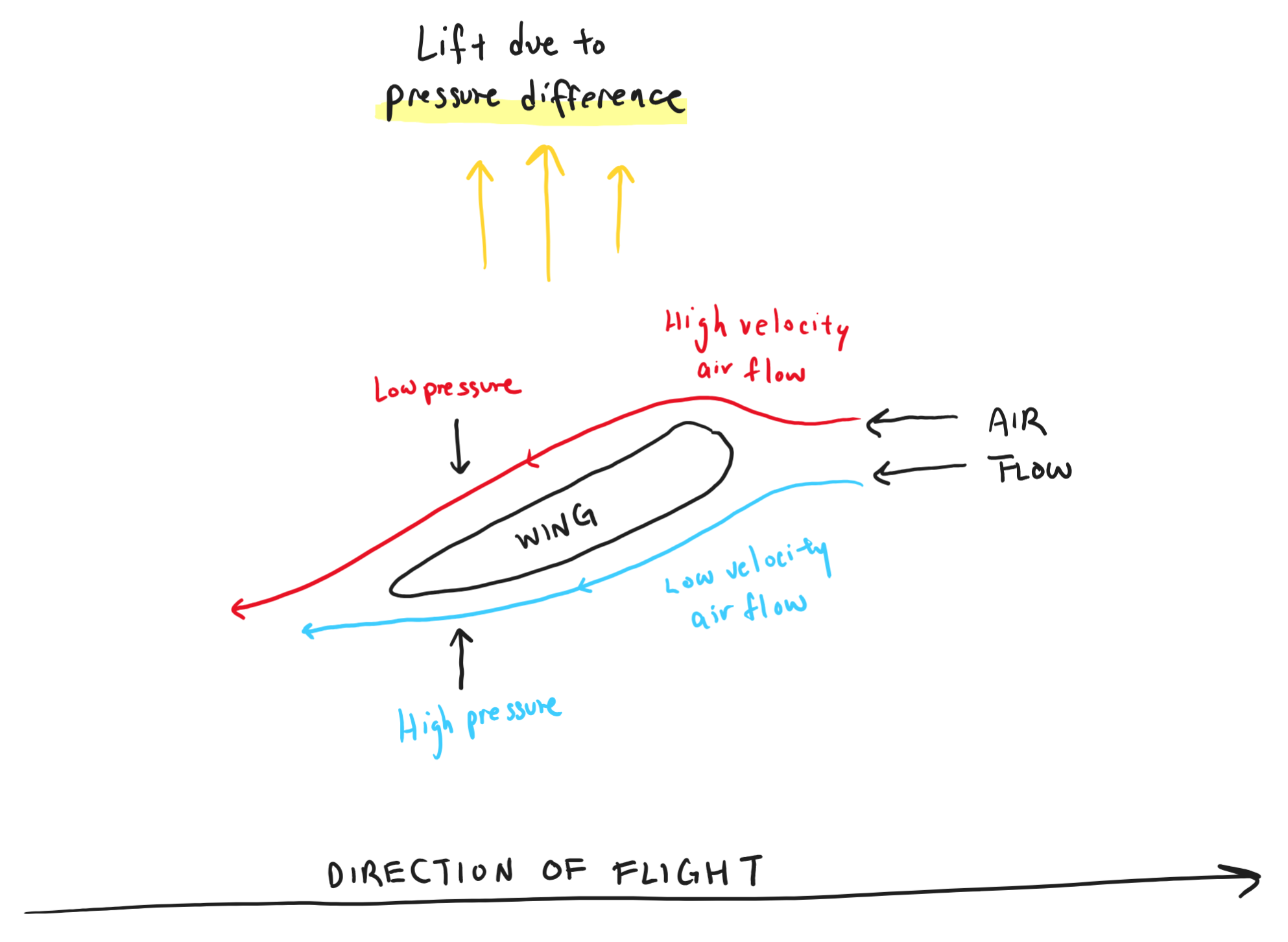
By creating a low-pressure flow above the wings and a high-pressure flow below them, the air (which is the fluid in our case) moves toward the area of low-pressure, pressing into the bottom of the wing.
Using complex calculations made by real science-y scientists based on a plane's weight, material, etc., the plane generates enough air pressure difference to produce the lift needed for take off.
Birds that glide generally operate on the same physics as airplane wings. But there are also many types of birds that many types of wings.
I will skip bird anatomy, but in short, they have evolved to minimize weight to maximize efficiency.
TLDR: It is harder for something to take off if it is really heavy! Although some bird-like Pokémon seem like they should be able to fly, we also need to factor in the weight of the playable character.
In terms of Surf, the playable character rides on the back of the Pokémon swimming near the surface of the water
The key idea is that the Pokémon should at least be able to float, ensuring the playable character is not submerged. Why only float? In the video games, we can stop moving at any time, and we often battle other Pokémon trainers or wild Pokémon while stationary. Additionally, the speed at which the Pokémon swims is roughly similar to the swimming non-playable characters (NPCs).
- \( \rho =\) fluid density
- \( g =\) acceleration due to gravity
- \( V =\) fluid volume
A boat, for example, must overcome its weight force in water, like the previous example of the airplane in air. In this case, we use Archimedes' principle (AKA buoyancy or the buoyant force) to stay afloat in water, which equals to the weight force of the volume of the amount of fluid displaced.
- \( \rho =\) density
- \( m =\) mass
- \( V =\) volume
Density is the relationship between mass and volume. Simply put, an object that is more dense will have more difficulty floating than one that is less dense. For example, consider two cubes at 10 kilograms but differing in size:
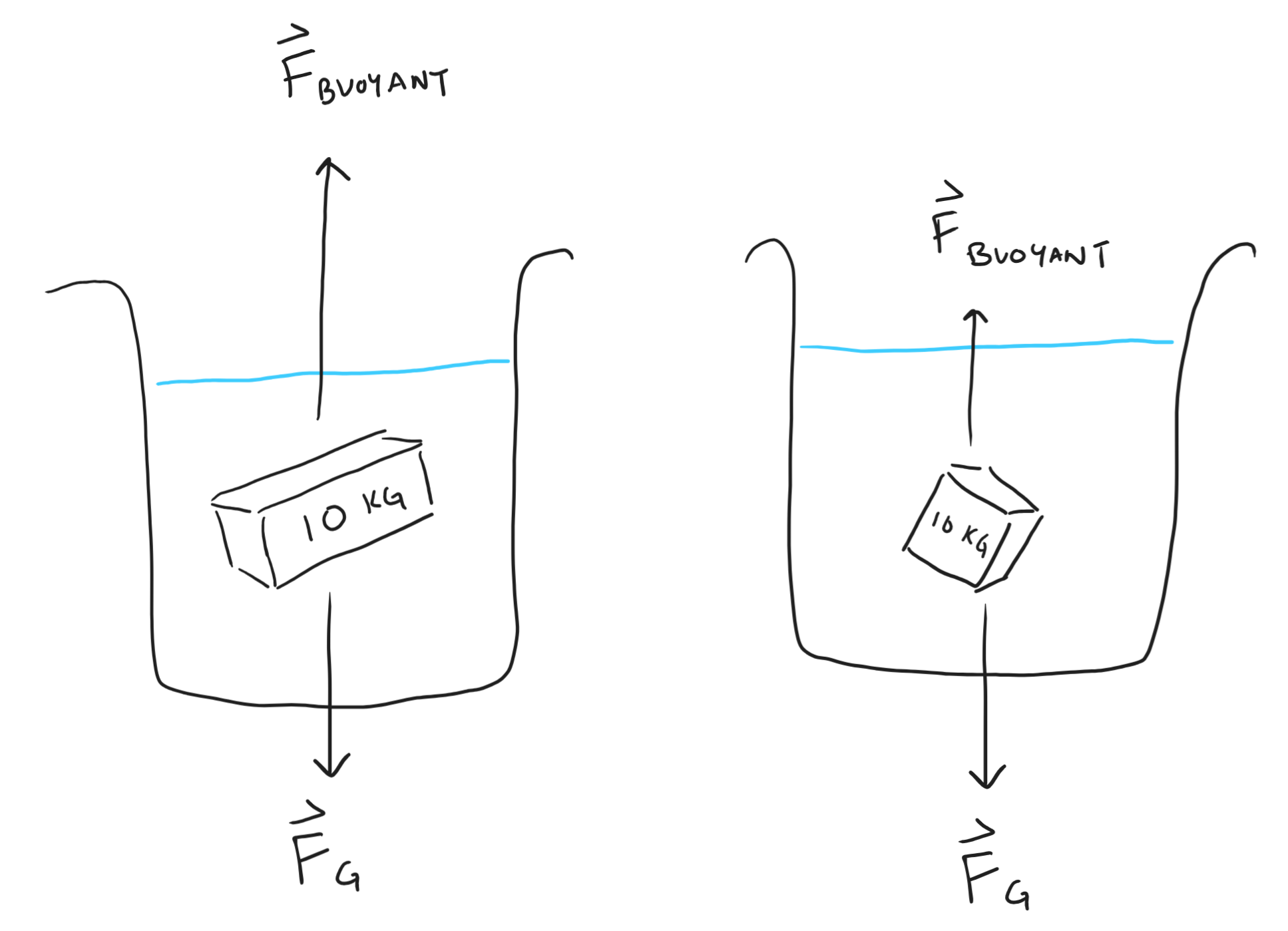
The larger cube has a greater volume and displaces more water. And so, it experiences a larger buoyant force.
If the buoyant force equals the weight force, an object will stay submerged and suspended in the water at the depth it was placed. To float and rise towards the surface, the buoyant force must exceed the weight force, which requires the object to have a large volume and low density.
I will skip the anatomy of sea creatures, but many types of fishes, for example, have a swimmbladder. This is an internal organ filled with gases that is used to change the fish's overall density and modulate buoyancy.
And that's why large ships can float!
- Spread total mass over large surface area
- Inner compartments inside boat are filled with air
- Air is far less dense than water
- Thus lowering overall density
TLDR: In water, we need to factor in both weight and volume. Altogether, the Pokémon must be less dense such that, after adding the weight of the playable character, we can stay afloat.
📈 Early Ideation
I used python and BeautifulSoup4 to get Pokémon data from Bulbapedia, a community-driven encyclopedia for Pokémon, and used gspread to write the data to Google Sheets. These two tasks alone took me almost three days because I had to account for all possible cases when retrieving data. For example, navigating the naming conventions for both Pokémon and the html elements on a page, as well as determine where these html elements were located.
Using the Bulbapedia's List of Pokémon by National Pokédex number, I recorded the following data for each of all 1025 Pokémon:
- Whether they have different forms (same species but differ in appearances: regional forms, evolutional forms, transformations, etc.)
- Abilities (allow for special passive effects or specific mechanics that may describe parts of their biology and how they interact with the world)
- Types (elemental attributes)
- Height (in metres)
- Weight (in kilograms)
- Whether they can learn Surf
- Whether they can learn Fly
- Body shape (categorization of a Pokémon's body shape/type)
Now, let's dive into the calculations. Again, full credits to adef as I mostly followed his work.
When evaluating for Fly, adef used real-life bird data. For Surf, it became a little more complicated. As we know, density is related to volume, and Pokémon metrics provide limited data to work with.
adef approximated each Pokémon's volume using the formula for cylinder, and therefore also estimated the radius of each Pokémon. He assigned a value called the radius-to-height ratio, which estimated the radius as a fraction of the height. Similarly, I assigned up to four ratios per body shape category. This task also took a while because I eyeballed each Pokémon in each shape category. Since proportions can vary widely, using a single ratio for each body shape would not accurately account for all Pokémon in that category.
Seriously, eyeballing was my last resort. I tried my best to calculate a more accurate radius for every Pokémon.
The 3D models had long been extracted from the video games. I did try opening them in Blender and was able to view the height, length, width, volume, and calculated density of the mesh model. However, it was not efficient for me to download, import each into Blender, and then find the dimensions of the model. In addition, I am not proficient with 3D-modelling or Blender, so off of a quick Google search I could not find a fast way to extract only the dimensions.
Another approach I considered was approximating the length based on image dimensions. For example, this page on a website called ProjectPokemon has a GIF of each 3D model that is forward-facing at an angle. I could easily get the rendered size of the img element and use simple algebra to get an approximate value for the radius. However, for certain body shapes like serpentine, the proportions of their elongated bodies could not be accurately reflected.
Ultimately, I gave up, haha. adef even mentioned that he manually went through each Pokémon and assigned a ratio by hand. I knew I did not want to do that, so I tried identifying patterns for each body shape instead.
Some shape categories were easy and had consistent proportions such that one ratio was sufficient. For example, the category of Pokémon consisting of only a head all were fairly spherical in shape, so I let the ratio be 0.5. For other shapes, like bipedal, serpentine, or winged, not all Pokémon that fell into these categories had consistent proportions. Therefore, I assigned different ratios based on a few notable height points. This is reflected in my python code.
With a radius calculation for each Pokémon, I was able to compute their volumes and densities.
🔬 Testing
Birds of the World by the Cornell Lab of Ornithology has a whole comprehensive database on the various birds that exist on Earth. adef used this to mathematically assess whether a Pokémon should be able to fly. He gathered the height and weight of 50 different bird species, and used a power series to generate an equation where weight was the independent variable and height (or expected height) was the dependent variable. The assumptions were that a Pokémon's wingspan was proportional to its height, and this relationship scaled linearly across all Pokémon.
Fortunately, All About Birds by the Cornell Lab has many birds available to view for free. To ensure a diverse selection of birds from around the world, I used the list of bird cards from Wingspan, a board game that featured real bird species. Then, I made another data-scrapping algorithm to extract the bird data from All About Birds, plotted the data points, and generated my own power series equation.
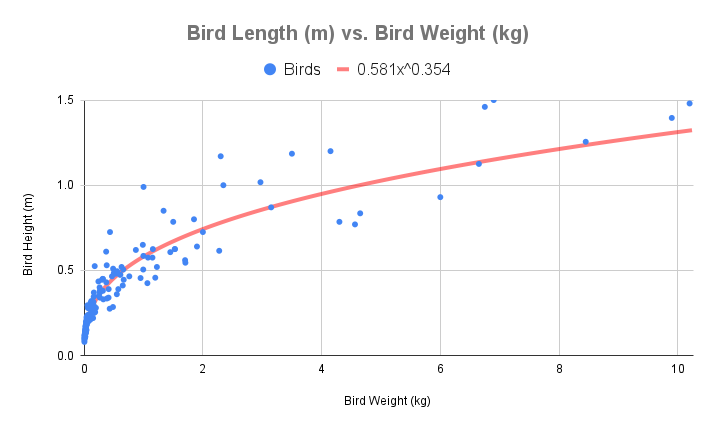
- adef's equation: \(y = 0.532x^{0.343}\)
Important note: the terms "length" and "height" were used interchangably. On the Cornell Lab websites, they utilized "length", "weight", "wingspan", etc. However, a Pokémon's dimensions are always labeled as height and weight, and it is safe to assume that the height value equated to a Pokémon's length if it had a long body or large wingspan. Let's look at a few examples:
Pikachu, the Mouse Pokémon

- Height: 1'04" or 0.4 m
- Weight: 13.2 lbs. or 6.0 kg
- Body shape: Quadruped
As a relatively small quadruped creature, it is safe to assume that the height of Pikachu is measured from its feet to head (or maybe ears).
Charizard, the Flame Pokémon

- Height: 5'07" or 1.7 m
- Weight: 199.5 lbs. or 90.5 kg
- Body shape: Tailed bipedal
For a dragon-like creature who stands upright, it is safe to assume that the listed height is its height.
Golbat, the Bat Pokémon

- Height: 5'03" or 1.6 m
- Weight: 121.3 lbs. or 55.5 kg
- Body shape: Single pair of wings
A bat with a vertical height of 1.6 metres would be almost as tall as Charizard, and overall just scarily, crazily large... Seriously, just look at a regular picture of Golbat.

We should (nay, need) to assign the height as a measurement of its length (or wingspan).
Gyarados, the Atrocious Pokémon

- Height: 21'04" or 6.5 m
- Weight: 518.1 lbs. or 235.0 kg
- Body shape: Serpentine

Again, the value of its height really should be the measurement of its entire length. There could be an argument that its height could be measured from where its segmented body touches the ground. However, technically it could place itself anywhere along its body, and even then, that would be one tall leviathan-like creature... It is way safer to assume 6.5 metres is the length of its serpentine body.
Eternamax Eternatus, the Gigantic Pokémon

- Height: 328'01" or 100.0 m
- Weight: ???
- Body shape: Serpentine
There is no way 100 metres is anything other than the length measurement of its entire serpentine body.
Then, an expected height was calculated for each Pokémon and was compared with the Pokémon's listed height. In addition, a second expected height was calculated after adding the playable character's weight with the Pokémon's listed weight.
For Surf, adef used the radius ratio to approximate a radius for each Pokémon. This value was then used to calculate the volume of each Pokémon using the formula for a cylinder: \(V = \pi r^2 h\), where \(r =\) radius and \(h =\) height. Following that, the density was calculated and compared to the density of water \(\approx 1000 kg/m^3\).
Regarding the weight of the playable character, I assigned a value of 38 kg. In the Generation 4 Pokémon video games, the male protagonist was listed at 38 kg and the female protagonist 34 kg. Realistically, the value we should consider should be larger. In fact, the playable character can have as many or as few items in their bag that they carry with them at all times. Funnily enough, we can even store our bicycle! To give our lovable creatures a fair chance (and you will see why), we will stick with 38 kg.
⭐ Final Designs
Check out my Bulbapedia Web Scraper repository on Github!
It turns out that many Pokémon that can fly really should not be able to... On the other hand, majority of all Pokémon are impressively less dense! In addition to the 1025 official Pokémon, I added 200 form differences which yielded a total of 1225 Pokémon on my spreadsheet.
Out of 129 Pokémon capable of learning Fly, only 13 of them had an original height that matched or passed the expected height value... Yikes! Of those 13, only 10 were strong enough to carry the playable character. As well, 12 out of the 13 fliers are special and rare Pokémon that an average Pokémon citizen (who will never be a main character in a story) would likely not have regular access to them. Double yikes! Guess it is carbon emmissions or nothing!
By the waters, however, you may catch many average citizens with their Pokémon. Of the 266 Pokémon who can learn Surf, 251 can float, and 206 are capable of carrying the playable character. In fact, about 94% and 71% of all Pokémon can float in water and carry the playable character, respectively! Whether they would actually enjoy being in water... Well, that is a question for another time...
The Fly numbers are quite disheartening. Let's stretch the confines of what Pokémon can be considered a potential flyer by including 3 additional criteria:
- Ability
A Pokémon's ability can be described as special passive effect(s) or specific mechanic(s) that may influence battles or the overworld. Levitate is an ability that insinuates the Pokémon is able to hover, float or levitate above the ground. - Type
A Pokémon's type is its elemental attribute, with each Pokémon having up to two types for any given form. The Flying type is assigned to practically all aeronautical and flight-themed (e.g. bird-like, dragon-like, winged-insects) Pokémon. And besides, Fly is literally in the name! - Body shape
The body shape is a categorization of a Pokémon's physical body shape. I considered three specific shapes:- Pokémon consisting of only a head
- Pokémon with a single pair of wings
- Pokémon with two or more pairs of wings
The new additions expanded the pool to a new total of 247 potential fliers (i.e. Pokémon that can learn the move Fly, can have the ability Levitate, are or are part Flying type, or have wings or consist only of a head). Unfortunately, this only added 11 new Pokémon to the list of those with an original height at or greater than their expected height value, for a grand total of just 24. Wow.
But hey, at least we now have a broader selection of viable fliers beyond just the special Pokémon I mentioned earlier! Here are a few of them:
- Galarian Weezing = 193% of its expected height
- Gyarados = 162% of its expected height
- Skiploom = 103% of its expected height
- Dragapult = 129% of its expected height
- Flutter Mane = 147% of its expected height
Sadly, only half of the 24 are large enough to carry the playable character. To take it another step further, I also looked at all Pokémon that had at least 80% of their expected height. This brought the total to 41 viable fliers, but only 15 could carry the playable character. Well, I guess we better not take them for granted! Here are a some of the new-new additions to the 41 fliers:
- Mega Pidgeot = 94% of its expected height
- Xatu = 99% of its expected height
- Masquerain = 87% of its expected height
- Mega Altaria = 88% of its expected height
- Gliscor = 91% of its expected height
- Sigilyph = 95% of its expected height
- Drampa = 81% of its expected height
- Corviknight = 82% of its expected height
💭 Next Steps
Yeah, not a lot of fliers... but tons of floaters! But of course, we should take this with a grain of salt. After all, Pokémon is a fictional universe and it is fair to bend some real-life scientific rules.
We should also give the Pokémon creators some grace because they likely were not thinking too deeply about these metrics when designing them.
There also exists size and weight variation, where different Pokémon of the same species can vary in these attributes. This is a relatively modern mechanic introduced in games like Pokémon GO and the Let's Go games. With this variability in mind, we can reasonably assume that most Pokémon with wings should theoretically be able to fly.
Whether they should or should not be able to carry an average citizen... Let's just say we better start doubling or tripling up on our fliers...
Back in 🔖 early ideation in an optional part, I mentioned that I tried retriving the dimensions from the 3D models of the Pokémon. As a next step for me, I think I would love to know more and gain experience in 3D modelling and 3D graphics software.
Otherwise, I would love to examine utilizing Pokémon as general transportation (e.g. traverse terrain). There are plenty of Pokémon who have real-life animal counterparts. I think it would be fun to also look at all the Pokémon that seem ridable (e.g. horse-like, large dog-like and strong humanoid Pokémon).